Lògica de programació
Introducció a la lògica de programació, amb explicacions clares i exemples pràctics per desenvolupar el pensament computacional des de zero.
Introducció
La lògica de programació és la base sobre la qual es construeixen tots els programes informàtics. Abans d’aprendre a programar directament en un llenguatge de programació concret, és fonamental comprendre com s’estructuren i es resolen els problemes de manera lògica i seqüencial. Aquest procés mental s’anomena pensament computacional, i aprendre a desenvolupar-lo és el primer pas per convertir idees en solucions digitals.
Coneixements previs
Referències
- Gómez Jiménez, E. & Aguilera Jinesta, R. (2023). Metodología de la programación: conceptos, lógica e implementación. Marcombo. ISBN: 978‑8426735935.
- Knuth, D. E. (2022–2025). The Art of Computer Programming, Volúmenes 4A/B y fascículos recientes. Addison-Wesley.
Índex
- Pensament computacional: una habilitat clau
- Com es resolen problemes amb lògica
2.1. Anàlisi del problema
2.2. Descomposició i passos seqüencials
2.3. Reconeixement de patrons i generalització
2.4. Disseny de solucions pas a pas - Recomanacions per resoldre exercicis de lògica
- Exercicis
1. Pensament computacional: una habilitat clau
Abans d’aprendre a programar, a resoldre exercicis o a escriure instruccions pas a pas, és important comprendre una capacitat fonamental: el pensament computacional. No es tracta només de saber utilitzar ordinadors o escriure codi, sinó de desenvolupar una manera de pensar per resoldre problemes de forma lògica, estructurada i eficient.
El pensament computacional és una habilitat que ens permet entendre problemes complexos i trobar solucions que puguin ser aplicades per una persona, una màquina o ambdues. Es basa en la lògica, l’anàlisi i la creativitat, i és una manera de pensar que no depèn d’un llenguatge de programació concret, sinó de com organitzem les nostres idees per resoldre tasques pas a pas.
- Descomposició: dividir un problema gran en parts més petites i manejables.
- Reconeixement de patrons: identificar similituds i estructures comunes entre problemes.
- Abstracció: centrar-se en els elements essencials i descartar els detalls que no són rellevants.
- Algorismes: dissenyar passos clars i ordenats que permetin resoldre el problema de manera precisa.
Aquestes habilitats no només serveixen per programar. També s’apliquen en àrees com les matemàtiques, les ciències, la tecnologia, el disseny, l’enginyeria o fins i tot en la vida quotidiana (per exemple, a l’hora de planificar una recepta de cuina o organitzar una ruta de viatge).
El pensament computacional és una competència molt necessària al segle XXI perquè:
- Fomenta el raonament lògic i la resolució de problemes.
- Desenvolupa l’autonomia i la capacitat de prendre decisions estructurades.
- Prepara l’alumnat per treballar en equip, comunicar solucions i afrontar desafiaments tècnics.
- No es limita a la informàtica: és útil en qualsevol context que requereixi organitzar informació, trobar solucions o prendre decisions.
2. Com es resolen problemes amb lògica
Resoldre problemes amb lògica no vol dir memoritzar fórmules o aplicar receptes mecàniques, sinó aprendre a observar, pensar i actuar amb un pla. La lògica ens ajuda a prendre decisions raonades, trobar patrons i dissenyar solucions pas a pas, sense deixar-nos portar per la intuïció o la improvisació.
Quan ens enfrontem a un problema —ja sigui a classe, a casa o a la feina— solem passar per una sèrie de fases. Aprendre a identificar aquestes etapes i aplicar-les amb ordre és clau per desenvolupar la nostra capacitat de raonament.
2.1. Anàlisi del problema
Abans d’intentar resoldre qualsevol problema, és fonamental entendre què se’ns està demanant exactament. Aquest primer pas pot semblar evident, però moltes vegades fallem per no aturar-nos prou a pensar i llegir amb atenció.
L’anàlisi del problema consisteix en:
- 🔍 Comprendre l’enunciat
Llegir detingudament el problema i assegurar-nos que entenem tota la informació rellevant. Preguntar-nos:
- Quines dades ens dona el problema?
- Què hem d’obtenir com a resultat?
- Quines condicions o limitacions se’ns imposen?
De vegades, el problema és extens, està redactat amb paraules ambigües, generals o conté informació que no és important. En aquest cas, és útil reformular-lo amb les nostres pròpies paraules, fer preguntes, o fins i tot subratllar la informació més important.
- 📌 Identificar el que és rellevant
No totes les dades que apareixen en un problema són necessàries. Aprendre a distingir entre l’essencial i l’accessori forma part del pensament lògic. Si no filtrem bé la informació, podem distreure’ns o dissenyar solucions errònies.
- 🧩 Dividir el problema
Quan un problema sembla molt complex, el millor és dividir-lo en parts més petites. Resoldre pas a pas cada fragment acostuma a ser més fàcil i, al final, podem connectar les solucions parcials per resoldre el conjunt.
- 💡 Pensar en possibles camins
En aquesta etapa encara no escrivim solucions definitives. És el moment d’explorar idees, plantejar hipòtesis, imaginar què passaria “si…” i visualitzar el camí que ens pot portar del punt de partida al resultat final.
🧠 Exemple senzill:
Suposa que has d’organitzar l’horari d’estudi d’una setmana.
El problema sembla simple, però requereix pensar:
- Quantes hores lliures tinc?
- Quines assignatures he de prioritzar?
- Hi ha dies en què no puc estudiar?
- Com divideixo el temps sense saturar-me?
Analitzar-ho et permet prendre decisions lògiques en lloc d’improvisar o copiar l’horari d’una altra persona.
2.2. Descomposició i passos seqüencials
Un dels principis clau per resoldre qualsevol problema amb lògica és la descomposició. Aquesta consisteix a dividir un problema gran en parts més petites, més fàcils d’entendre i de resoldre.
Quan intentem abordar un problema complex de cop, ens podem bloquejar o cometre errors. En canvi, si el fragmentem en passos, es torna més manejable.
- 🔹 Què implica descompondre un problema?
D’un problema general o gran, haurem de:
- Separar cada tasca o acció necessària.
- Identificar un ordre lògic per executar cada pas.
- Treballar amb parts independents, però connectades entre si.
🧠 Exemple:
Problema: Preparar un entrepà.
Encara que sembli trivial, requereix una sèrie de passos ordenats:
- Anar a la cuina.
- Agafar dues llesques de pa.
- Afegir els ingredients desitjats (pernil, formatge, etc.).
- Juntar les llesques.
- Servir l’entrepà en un plat.
Cada una d’aquestes accions es pot tractar com una unitat independent. I si l’objectiu canvia (fer un sandvitx calent o un de vegetal), només alguns passos es modificaran. Això és el que fa útil la descomposició.
- 🔄 Seqüencialitat
Un cop descompost, l’ordre importa. No pots servir l’entrepà si encara no l’has muntat. Aquest principi, anomenat flux seqüencial, és la base de molts algorismes i tasques quotidianes.
2.3. Reconeixement de patrons i generalització
Un altre aspecte essencial del pensament lògic és la capacitat d’observar similituds entre problemes i extreure’n regles generals que es puguin reutilitzar.
Això es coneix com a:
- Reconeixement de patrons: detectar estructures, seqüències o comportaments que es repeteixen.
- Generalització: extreure principis o regles a partir de casos concrets.
🧠 Exemple:
Imagina aquests tres problemes:
- Comptar de 1 a 10.
- Comptar de 5 a 15.
- Comptar de 20 a 30.
Tot i que els números canvien, el patró és el mateix: “sumar 1 a cada pas fins arribar a un número final”. Reconèixer aquest patró permet generalitzar una solució que serveixi per a qualsevol interval.
🎯 Per què és útil?
- Evita resoldre des de zero problemes similars.
- Permet crear solucions adaptables i reutilitzables.
- Enforteix el pensament abstracte, clau en matemàtiques i programació.
2.4. Disseny de solucions pas a pas
Un cop hem analitzat el problema, l’hem descompost en parts i hem detectat patrons, arriba el moment de dissenyar una solució lògica pas a pas.
Aquest procés s’anomena disseny algorísmic. Tot i que encara no estiguem escrivint codi, ja estem creant una seqüència d’accions que resolen el problema. És com escriure una recepta: cada pas ha de tenir sentit, estar ben ordenat i ser comprensible.
🔸 Característiques d’una bona solució pas a pas:
- Claredat: cada pas és concret, sense ambigüitats.
- Ordre: els passos segueixen una lògica que condueix al resultat.
- Eficiència: s’evita repetir tasques innecessàries.
- Adaptabilitat: si el problema canvia, es pot modificar la solució sense haver-la de refer completament.
🧠 Exemple:
Problema: Calcular la mitjana de tres notes.Disseny de la solució:
- Demanar a l’usuari que introdueixi les tres notes.
- Sumar les tres notes.
- Dividir el total entre 3.
- Mostrar el resultat.
Aquest disseny es pot representar més endavant amb un llenguatge de programació, pseudocodi o diagrama. Però la seva estructura lògica ja és vàlida.
Resoldre exercicis de lògica no es tracta només d’arribar a una resposta correcta, sinó d’aprendre a pensar de manera estructurada i ordenada. A continuació et deixem una sèrie de recomanacions que t’ajudaran a treballar els exercicis de forma més eficaç, evitant bloquejos i desenvolupant el teu raonament pas a pas.
3. Recomanacions per resoldre exercicis de lògica
Sembla obvi, però moltes vegades els errors apareixen per no llegir bé el que es demana. Abans de fer res, assegura’t d’entendre el problema:
- Quina informació es dona?
- Què s’està demanant?
- Hi ha condicions, restriccions o passos ocults?
Si fa falta, llegeix més d’una vegada o subratlla el que és important.
De vegades, explicar el problema “a la teva manera” t’ajuda a comprendre’l millor. Intenta expressar-ho com si ho expliquessis a algú que no ho coneix. Això t’obliga a identificar el que és essencial.
També pots fer un esquema, llista o dibuix si el problema és visual o numèric.
No intentis resoldre-ho tot de cop. Pensa:
- Puc resoldre una part abans que una altra?
- Quins passos intermitjos necessito?
Resoldre petites parts et donarà confiança i claredat per afrontar la resta de l’exercici.
En els exercicis de lògica (i en la programació), l’ordre importa. Cada pas ha de basar-se en l’anterior i preparar el següent.
Intenta pensar com si estiguessis escrivint una recepta: Què ha de passar primer? Què ve després?
És normal quedar-se bloquejat. Quan passi:
- Torna a llegir l’enunciat.
- Revisa el que ja has fet.
- Prova amb un exemple més senzill.
- Demana ajuda, però explica el teu raonament primer.
Moltes vegades el simple fet de repassar el que has fet et permet veure l’error.
Una bona manera de saber si el teu raonament és correcte és provar-ho amb casos reals o inventats. Si funciona en diversos casos, probablement és una bona solució.
També pots preguntar-te:
“Aquest pas funcionaria si el número fos negatiu? O si fos zero?”
No n’hi ha prou amb arribar al resultat: cal expressar el procés de manera comprensible. Si algú més llegeix la teva solució, hauria de poder seguir-la sense dificultats.
- Utilitza frases breus.
- Numera els passos si cal.
- Evita salts de lògica o suposicions no explicades.
Cada error és una oportunitat per millorar el teu raonament. Quan revises una solució incorrecta:
- Analitza quina part ha fallat.
- Intenta entendre per què vas cometre aquest error.
- Torna-ho a intentar, sense copiar directament la resposta.
4. Exercicis
4. Exercicis
A continuació es plantegen diferents exercicis per practicar la lògica de programació classificats segons el nivell de dificultat. Aquests exercicis es poden resoldre mitjançant qualsevol llenguatge de programació, pseudocodi o diagrames de flux. La idea és que cada exercici ajudi a desenvolupar la capacitat de raonament lògic i a aplicar els conceptes apresos.
4.1. Dificultat bàsica ✅
Els exercicis proposats en aquest nivell són ideals per a aquelles persones que estudien programació per primera vegada i no tenen coneixements previs. Cada exercici està pensat per desenvolupar habilitats bàsiques en la resolució de problemes, de manera que caldrà aplicar pensament lògic i utilitzar estructures elementals de programació.
Exercici 1: El meu primer programa v.1
✨ Escriu un programa que mostri el següent missatge en pantalla:
Hola món!
Exercici 2: Salutació personalitzada
Fes un programa que mostri una salutació personalitzada a l’usuari.
- 👤 Declara una variable per emmagatzemar el nom d’una persona.
- 🧑💻 Demana a l’usuari que introdueixi el seu nom.
- 💬 Mostra un missatge de salutació personalitzat en pantalla, per exemple:
Hola, Josep!
Exercici 3: Calculadora
🧮 Demana dos números decimals a l’usuari i mostra el resultat de les següents operacions:
- ➕ Suma
- ➖ Resta
- ✖️ Multiplicació
- ➗ Divisió
⚠️ Important! No és possible fer una divisió entre zero.
Si això passa, el programa ha de mostrar un missatge d’advertència i evitar el càlcul.
Exercici 4: Calculadora avançada
🧮 Demana un número decimal a l’usuari i mostra el resultat de les operacions matemàtiques següents:
- Valor absolut
- Arrel quadrada
- Potència (elevat al quadrat)
- Mòdul
- Cosinus
- Sinus
- Tangent
Exercici 5: Àrea d’un rectangle
Fes un programa que calculi l’àrea d’un rectangle.
- 📐 Demana a l’usuari la base i l’alçada d’un rectangle.
- 🧠 Calcula la seva àrea utilitzant la fórmula:
Àrea = base × alçada - 📊 Mostra el resultat per pantalla.
Exercici 6: El meu primer programa v.2
Millora l’exercici 1, per ▶️ demanar a l’usuari la paraula Iniciar
- 🔹 Si s’introdueix correctament, mostrarà:
Hola món! - 🔸 Si s’introdueix qualsevol altre valor, mostrarà:
Fi del programa
Exercici 7: Semàfor
🚦 Demana a l’usuari que introdueixi una de les paraules següents: "Verd", "Ambre" o "Vermell".
Segons el valor introduït, el programa ha de mostrar:
- 🟢 Verd →
Pots passar - 🟡 Ambre →
Passa si no hi ha perill - 🔴 Vermell →
Atura’t
Exercici 8: Número parell o senar
Fes un programa que faci el següent:
- 🔢 Demana un número enter a l’usuari.
- 📋 Mostra un missatge que indiqui si el número introduït és parell o senar.
Exercici 9: El meu primer programa v.3
Millora l’exercici 6, per ▶️ demanar a l’usuari la paraula clau: Iniciar i segons l’entrada de l’usuari:
- ✅ Si s’introdueix la paraula correcta, es demanarà a l’usuari un número enter positiu.
- 🔁 El missatge
Hola món!es mostrarà tantes vegades com el número introduït. - ❌ Si la paraula inicial no és vàlida o el número no és positiu, es mostrarà el missatge:
Fi del programa.
Exercici 10: Comptador i Compte enrere
Fes un programa que faci el següent:
- 🔢 Demana un número enter a l’usuari.
- 🔁 Utilitza un bucle per mostrar per pantalla els números de l’1 al número introduït de forma seqüencial.
- ⏳ Utilitza un altre bucle per mostrar per pantalla els números del número introduït a l’1 de forma decreixent.
- ❌Si el número introduït és menor que 1, mostra un missatge d’error:
El número ha de ser més gran o igual a 1.
Exercici 11: Suma acumulada
Fes un programa que faci el següent:
- 🧑💻 Demana a l’usuari que introdueixi cinc números enters.
- ➕ Calcula la suma total de tots ells.
- 📊 Mostra el resultat final per pantalla.
Exercici 12: El més gran de tres números
Fes un programa que faci el següent:
- 🔢 Demana tres números a l’usuari.
- 🔍 Compara els valors introduïts i mostra quin és el més gran dels tres.
Exercici 13: Taula de multiplicar
Crea un programa que faci el següent:
- ✖️ Demana un número a l’usuari.
- 🔁 Mostra la seva taula de multiplicar de l’1 al 10.
- 📋 El format a mostrar ha de ser com:
1 x 1 = 1 - ❌ Si el número introduït no és vàlid, mostra un missatge d’error:
El número ha de ser més gran o igual a 1.
Exercici 14: El meu primer programa v.4
Millora l’exercici 9, per incloure la funcionalitat bàsica dins d’un procediment, tal com s’indica a continuació:
- 🧩 Escriu un procediment que rebi com a paràmetre un número enter positiu.
- 💬 Aquest procediment ha d’imprimir
Hola món!tantes vegades com indiqui el número rebut. - 🔁 El procediment no ha de retornar cap valor, només mostrar el missatge per pantalla.
El programa principal haurà de:
- ▶️ Demanar a l’usuari la paraula
Iniciar. - ✅ Si la paraula és correcta, demanarà un número enter positiu i cridarà el procediment.
- ❌ Si s’introdueix qualsevol altre valor o el número no és vàlid, mostrarà:
Fi del programa.
Exercici 15: Procediment per mostrar missatge
📝 Defineix un procediment anomenat MostrarMissatge que imprimeixi un missatge motivador per pantalla.
▶️ Crida aquest procediment des de l’algorisme principal per mostrar-lo.
Exercici 16: Arrodoniment d’un número decimal
Fes un programa que compleixi el següent:
- 🔢 Demana a l’usuari un número decimal.
- 🔄 Utilitza una funció d’arrodoniment per convertir-lo en un número enter.
- 📊 Mostra el resultat per pantalla.
Exercici 17: Llista de la compra
Fes un programa que faci el següent:
- 🛒 Crea un array de 5 elements.
- ✍️ Demana a l’usuari que introdueixi una data i els productes que necessita comprar.
- 📋 En acabar, mostra la data indicada i el llistat complet per pantalla.
Exercici 18: Mitjana d’elements en un array
Fes un programa que faci el següent:
- 🔢 Crea un vector (array) de 10 números.
- ✍️ Demana a l’usuari que introdueixi els valors un a un.
- 📊 Calcula i mostra la mitjana dels elements emmagatzemats a l’array.
Exercici 19: Matriu aleatòria
Desenvolupa un programa que faci el següent:
- 🔢 Crea una matriu 5x5 de tipus numèric.
- 🎲 Inicialitza tota la matriu amb números aleatoris compresos entre 1 i 10.
- ➕ Recorre tota la matriu i calcula la suma total de tots els seus elements.
- 🖥️ Mostra el resultat de la suma per pantalla.
Exercici 20: Taulell d’escacs
Crea un programa que permeti representar un taulell d’escacs.
- ♟️ Crea una matriu que representi el taulell d’escacs (8x8).
- 🏰 Col·loca totes les peces en les seves posicions inicials per a cada jugador. Cada jugador disposa de:
- ♚ Un rei (R)
- ♛ Una dama (D)
- ♜ Dues torres (T)
- ♞ Dos cavalls (C)
- ♝ Dos alfilers (A)
- ♙ Vuit peons (P)
🎨 Per distingir cada jugador, s’afegirà una lletra:
- ⬜ B per al jugador Blanc.
- ⬛ N per al jugador Negre.
📌 Per exemple, el rei del jugador blanc es representarà com B-R, i el del negre com N-R.
4.2. Dificultat fàcil ⚠️
En aquest nivell, els enunciats no especifiquen de forma explícita quines estructures bàsiques s’han d’utilitzar. Es comença a potenciar el pensament lògic, explorant diferents solucions possibles i determinant com arribar a la resolució del problema de manera eficient.
Exercici 21: Joc Fizz Buzz
🎮 Escriu un programa que imprimeixi 🖥️ els números de l’1 al 100, un per línia.
🚨 Tanmateix, hauràs de substituir certs números segons aquestes regles:
- 🔺 Múltiples de 3 → mostrar
"fizz" - 🔹 Múltiples de 5 → mostrar
"buzz" - 🧨 Múltiples de 3 i 5 → mostrar
"fizzbuzz"
📌 Exemple de com comença la seqüència: 1, 2, Fizz, 4
Exercici 22: Àrea d’un polígon
📐 Crea una única funció que rebi com a paràmetre un tipus de polígon i calculi la seva àrea segons els seus components.
✅ Només es processarà un polígon per crida.
Els polígons permesos són:
- 🔺 Triangle
- ◼️ Quadrat
- 🟥 Rectangle
🖥️ Mostra per pantalla l’àrea calculada.
Exercici 23: Invertir cadena
🔄 Crea un programa que inverteixi l’ordre dels caràcters d’una cadena de text.
🚫 No pots utilitzar funcions pròpies del llenguatge que ja ho facin automàticament.
📌 Per exemple: "Hola món" → "nóm aloH"
Exercici 24: Convertidor de decimal a binari
💡 Crea un programa que transformi un nombre decimal al seu equivalent en binari.
🚫 No facis servir funcions incorporades del llenguatge que facin aquesta conversió automàticament.
🧮 El resultat s’haurà de calcular mitjançant lògica de programació.
Exercici 25: Caràcters exclusius de cada cadena
✍️ Crea una funció que rebi dues cadenes com a paràmetres: str1 i str2.
🧵 La funció ha de generar dues noves cadenes:
- 🔹
out1: caràcters que estan astr1però no astr2 - 🔸
out2: caràcters que estan astr2però no astr1📋 Mostra ambdós resultats per pantalla.
Exercici 26: Factorial (n!)
🔢 Escriu una funció que calculi i retorni el factorial d’un nombre enter donat.
🧠 El factorial d’un nombre n (n!) es defineix com el producte de tots els enters positius des de l’1 fins a n.
📌 Per exemple: 3! → 1 * 2 * 3 = 6
Exercici 27: Validar nombre narcisista
🔍 Escriu una funció que determini si un nombre és un nombre narcisista o Armstrong.
🧮 Un nombre narcisista és aquell que és igual a la suma dels seus dígits elevats a la potència del nombre de dígits.
📌 Per exemple: 371 → 3^3 + 7^3 + 1^3 = 371
👉 Més informació: nombres narcisistes
Exercici 28: Paraules amb la primera lletra en majúscula
✍️ Crea una funció que rebi una cadena de text i converteixi la primera lletra de cada paraula en majúscula.
🚫 No pots usar funcions pròpies del llenguatge que ho facin directament.
Exercici 29: Calculadora de mil·lisegons
⏱️ Crea una funció que rebi quatre valors enters:
- Dies
- Hores
- Minuts
- Segons
🧮 La funció ha de calcular i retornar el total equivalent en mil·lisegons.
Exercici 30: Validar conjunts disjunts
🧩 Crea una funció que rebi dos arrays (conjunts) i determini si són conjunts disjunts, és a dir, si no comparteixen cap element en comú. ✅ Retorna true si són disjunts, o false en cas contrari.
📌 Per exemple:
- 👌
A [1,2,3] B [4,5,6]→true - ❌
A [1,2,3] B [3,4,5]→false
Exercici 31: Elements comuns o no comuns de dos conjunts
🔁 Crea una funció que rebi dos arrays i un valor boolean com a paràmetres.
📌 La funció ha de retornar un nou array segons la condició:
- ✅ Si el boolean és
true, retornarà els elements comuns entre ambdós arrays. - ❌ Si és
false, retornarà els elements que no es repeteixen en ambdós arrays.
🚫 No es poden utilitzar funcions pròpies del llenguatge que ho facin directament.
Exercici 32: Dibuixar quadrat o triangle
✏️ Crea un programa que dibuixi a la pantalla un quadrat o un triangle utilitzant asteriscs (*).
🔢 L’usuari haurà de:
- Indicar la mida del costat (enter positiu).
- Escollir si vol dibuixar un quadrat o un triangle.
Exercici 33: Validar vectors ortogonals
📐 Crea un programa que determini si dos vectors són ortogonals (és a dir, el seu producte escalar és igual a 0).
➕ Ambdós vectors han de tenir la mateixa longitud i representar-se com a arrays.
📌 Exemple: [1, -2] i [2, 1]
Exercici 34: Ordenar llistes numèriques
📊 Crea una funció que ordeni una llista de nombres segons el criteri indicat.
La funció ha de rebre:
- Una llista de nombres.
- Un paràmetre de tipus text:
"Asc"per ordre ascendent o"Desc"per ordre descendent.
🚫 No es permet utilitzar funcions pròpies del llenguatge que realitzin l’ordenació automàticament.
Exercici 35: Comptador de vocals
🔤 Crea una funció que rebi un text i compti el nombre de vocals (tant majúscules com minúscules).
📊 Mostra el resultat per pantalla.
Exercici 36: Marc quadrat de paraules
🖼️ Crea una funció que rebi un text i mostri cada paraula en una línia, tancada en un marc d’asteriscs.
📌 Exemple:
Entrada: "Hola, Món !"
Sortida:
*********** Hola, ** Món ** ! ***********Exercici 37: Convertidor de nombres romans a enters
🏛️ Crea un programa que converteixi nombres romans a enters.
- 📜 L’usuari ha d’introduir un nombre romà vàlid (per exemple,
XII,IV,XXI). - 🔢 El programa ha de retornar el valor enter corresponent.
🚫 No es poden usar funcions del llenguatge que facin la conversió automàticament.
Exercici 38: Convertidor de nombres enters a romans
🏛️ Crea un programa que converteixi nombres enters a nombres romans.
- 🔢 L’usuari ha d’introduir un nombre enter positiu (per exemple,
1,4,10). - 📜 El programa ha de retornar el nombre romà corresponent.
🚫 No es poden usar funcions del llenguatge que facin la conversió automàticament.
Exercici 39: Validar any de traspàs
📅 Crea una funció que rebi un any (nombre enter) i determini si és de traspàs o no.
ℹ️ Recorda que un any és de traspàs si és divisible per 4, però no per 100, excepte si també és divisible per 400.
Exercici 40: El segon nombre més gran
🔢 Donat un array de nombres, troba el segon nombre més gran de la llista.
⚠️ Assegura’t de contemplar que no tots els nombres siguin iguals i que l’array tingui almenys dos valors diferents.
Exercici 41: Convertidor de binari a decimal
💻 Crea un programa que converteixi un nombre binari al seu equivalent en decimal.
🚫 No es poden utilitzar funcions pròpies del llenguatge que ho facin automàticament.
Exercici 42: Càlcul del voltatge en un circuit elèctric
⚡ Crea una funció que calculi el voltatge segons la Llei d’Ohm.
La funció ha de:
- Rebre la intensitat (I) i la resistència (R)
- Calcular i retornar el voltatge (V = I × R)
- Retornar un missatge d’error si els valors són invàlids o insuficients
Exercici 43: Convertidor de temperatura
🌡️ Crea una funció que converteixi graus Celsius a Fahrenheit, i viceversa.
La funció ha de:
- Rebre el valor de la temperatura i la seva unitat d’origen
- Retornar el valor convertit a la unitat de destí
- Mostrar un missatge d’error si les dades són incorrectes o falten
Exercici 44: La vocal més comuna
🔤 Crea una funció que rebi un text i retorni la vocal més repetida.
⚠️ Tingues en compte:
- Majúscules i minúscules (no s’han de distingir)
- Vocals amb accent s’han de tractar com a equivalents (per exemple: á → a)
- En cas d’empat, pots retornar qualsevol de les vocals empatades
- Si no hi ha vocals, retorna buit
Exercici 45: Calendari d’advent
🎄 Crea una funció que rebi una data i analitzi la seva relació amb el calendari d’advent (de l’1 al 24 de desembre).
La funció ha de contemplar els següents casos:
- 📦 Si la data està dins del calendari: retornar el regal del dia i quants dies queden per acabar-lo.
- ⏳ Si la data és anterior a l’1 de desembre: indicar quants dies falten per començar.
- 📅 Si la data és posterior al 24 de desembre: indicar quants dies han passat des del seu final.
Exercici 46: La xifrat Karaca
🔐 Crea una funció que permeti xifrar i desxifrar text utilitzant l’algoritme de la xifrat Karaca.
El procés consisteix en:
- 🔄 Substituir cada vocal per un número:
a → 0,e → 1,i → 2,o → 3,u → 4 - ✅ Les consonants roman sense canvis
- ➕ Afegir una seqüència extra al final (per exemple,
aca) - 🔁 Invertir la cadena resultant
📌 Exemple:
Entrada: "Hola Mundo"
Resultat: "odnuM 3l0Haca"
Exercici 47: Multi convertidor d’unitats de mesura
📏 Crea un programa que permeti convertir entre diferents unitats de mesura.
- 🧮 L’usuari ha de poder triar entre:
- Longitud (metres, quilòmetres, milles)
- Pes (grams, quilograms, lliures)
- Temperatura (Celsius, Fahrenheit)
- 🔄 El programa ha de sol·licitar el valor a convertir i la unitat d’origen i de destí.
- 📊 Mostra el resultat de la conversió per pantalla.
Exercici 48: Sudoku simplificat 3x3
🎮 Crea un programa que permeti jugar a una versió simplificada del Sudoku, utilitzant una matriu de 3x3.
- 📐 El tauler es representa com una matriu bidimensional d’enters.
- Cada cel·la pot contenir un nombre de l’1 al 3 o estar buida (representada per
0o un espai). - 🔢 El programa ha de col·locar un únic nombre en una cel·la aleatòria com a pista inicial.
- 👤 Després, l’usuari introduirà els valors un a un, indicant la fila, la columna i el nombre a col·locar.
- ✅ S’ha de verificar que no hi hagi nombres repetits a la mateixa fila ni a la mateixa columna.
- 🔁 Després de cada intent, el tauler es mostrarà actualitzat amb els nombres introduïts.
- 🏁 El programa finalitzarà quan el tauler estigui complet i correcte, i mostrarà el tauler final i el nombre total d’intents.
Exercici 49: Endevina el nombre secret
🔐 Crea un programa que permeti jugar a endevinar un nombre secret generat aleatòriament per la màquina.
- 🎲 En començar, es generarà un nombre aleatori entre 1 i 100.
- 🎯 L’usuari intentarà endevinar-lo introduint nombres per teclat.
- 📈 Després de cada intent, el programa ha d’indicar si el nombre introduït és més gran o més petit que el nombre secret.
- 🔁 El joc continua fins que l’usuari encerti el nombre.
- 📊 Al final, es mostra el nombre total d’intents necessaris.
Exercici 50: Joc del penjat
🧩 Crea un programa que permeti jugar a endevinar una paraula secreta.
- 📜 El programa seleccionarà una paraula aleatòria d’una llista predefinida.
- 🔤 L’usuari haurà d’endevinar la paraula introduint lletres una a una.
- ❌ Si la lletra no està a la paraula, es mostrarà un missatge d’error.
- ✅ Si la lletra està, es mostrarà la seva posició dins la paraula.
- 🏁 El joc finalitza quan l’usuari endevina totes les lletres de la paraula.
4.3. Dificultat mitjana 🛠️
Els exercicis de dificultat mitjana requereixen combinar diverses estructures bàsiques i fer un ús més avançat del pensament lògic. Cal analitzar el problema en profunditat, identificar casos especials i optimitzar el procés per trobar solucions efectives. Aquí es fomenta la capacitat de planificació i la presa de decisions en la implementació. És possible que existeixi més d’una solució vàlida per a cada exercici, per la qual cosa s’anima a explorar diferents enfocaments, prioritzant aquells que siguin més òptims, clars i eficients.
Exercici 51: Joc del penjat amb nivells de dificultat
🧩 Crea un programa que permeti jugar a endevinar una paraula secreta.
- 📜 El programa sol·licitarà el nivell de dificultat (fàcil, mitjà o difícil)
- 🎚️ Segons el nivell:
- Fàcil: seleccionarà una paraula aleatòria de com a màxim 5 lletres d’una llista definida. El nombre d’intents serà 10.
- Mitjà: seleccionarà una paraula aleatòria entre 6 i 10 lletres d’una llista definida. El nombre d’intents serà 7.
- Difícil: seleccionarà una paraula aleatòria de més de 10 lletres d’una llista definida. El nombre d’intents serà 5.
- 🔤 L’usuari haurà d’endevinar la paraula introduint lletres una a una.
- ❌ Si la lletra no està a la paraula, es mostrarà un missatge d’error i es descomptarà un intent.
- ✅ Si la lletra està, es mostrarà la seva posició dins la paraula.
- 🏁 El joc finalitza quan l’usuari endevina totes les lletres de la paraula o es queda sense intents.
Exercici 52: Validar paraules anagrames
🔄 Escriu una funció que rebi dues paraules i retorni true o false segons siguin o no anagrames.
- ✍️ Un anagrama consisteix a formar una paraula reordenant totes les lletres d’una altra paraula inicial.
- 🧠 No cal comprovar si les paraules existeixen en un diccionari.
- 🚫 Dues paraules idèntiques no es consideren anagrames.
Exercici 53: Validador de nombres primers
🔍 Crea una funció que determini si un nombre enter positiu és primer.
- 📌 Un nombre primer és aquell que només és divisible per 1 i per ell mateix.
- 🚫 No pots usar funcions del llenguatge que realitzin la validació automàticament.
Exercici 54: Llistat dels 100 nombres primers
🧮 Escriu un programa que imprimeixi tots els nombres primers compresos entre 1 i 100.
Exercici 55: Comptador de paraules
📝 Crea un programa que compti quantes vegades es repeteix cada paraula i mostri el recompte final.
- ❌ Els signes de puntuació no formen part de la paraula.
- 🔠 Una paraula és la mateixa encara que estigui en majúscules o minúscules.
- 🚫 No es poden utilitzar funcions del llenguatge que resolguin el problema automàticament.
Exercici 56: Generador de codi Morse
🔤 Crea un programa que transformi text natural a codi Morse i viceversa.
- 🔍 El programa ha de detectar automàticament el tipus d’entrada i fer la conversió.
- 📡 En Morse s’utilitza: ratlla
—, punt., un espai" "entre lletres i dos espais" "entre paraules. - 🌐 Es pot usar l’alfabet Morse descrit a Viquipèdia – Codi Morse.
Exercici 57: Expressions equilibrades
🧩 Crea un programa que verifiqui si els parèntesis, claus i claudàtors d’una expressió estan equilibrats.
- ⚖️ Equilibrat significa que s’obren i es tanquen en l’ordre correcte.
- ➖ Tots els delimitadors tenen la mateixa prioritat.
✅ Exemple equilibrat: { [ a * ( c + d ) ] - 5 }
❌ Exemple no equilibrat: { a * ( c + d ) ] - 5 }
Exercici 58: Validador text palíndrom
🔁 Escriu una funció que rebi un text i retorni true o false segons sigui o no un palíndrom.
- 📖 Un palíndrom és una paraula o frase que es llegeix igual d’esquerra a dreta que de dreta a esquerra.
- 🚫 No s’han de tenir en compte els espais, signes de puntuació ni accents.
- ✅ Exemple vàlid: La ruta natural
Exercici 59: Cursa d’obstacles
🏃♂️ Crea una funció que avaluï si un/a atleta ha superat correctament una cursa d’obstacles.
Rep dos paràmetres:
- 📚 Un array de paraules:
"corre"o"salta". - 🛤️ Un string que representa la pista:
"_"per terra i"|"per tanca.
✅ Si fa corre en "_" o salta en "|", està correcte i avança.
❌ Si és diferent, falla. Es considerarà cursa fallida si hi ha tres faltes consecutives.
❌ Si la pista és més llarga que les accions del corredor, es considerarà cursa fallida.
⚠️ Si les accions del corredor són més que la pista, s’ignoraran les accions sobrants.
🔄 La funció retorna un booleà indicant si ha completat correctament la cursa.
Exercici 60: Calculadora del Màxim Comú Divisor (MCD) i el Mínim Comú Múltiple (MCM)
🔢 Crea dues funcions:
- 📏 Una per calcular el màxim comú divisor (MCD).
- 📐 Una altra per calcular el mínim comú múltiple (MCM).
🖥️ Des del programa principal crida les dues funcions per mostrar-ne el funcionament.
Exercici 61: Comptador guanyador del joc Pedra, Paper i Tisora
📝 Crea un programa que determini qui guanya més partides al joc de Pedra, Paper o Tisora.
- 📚 El programa obté dues llistes que representen cada jugada.
- Usa els caràcters: ✊
"R"(pedra), ✋"P"(paper), ✌️"S"(tisora). - 🏆 El resultat pot ser: “Jugador 1”, “Jugador 2” o “Empat”. A més, es mostrarà 🖥️ el nombre de partides guanyades.
Exercici 62: Simulador de màquina expenedora
🥤 Simula una màquina expenedora. El programa ha de gestionar el procés de compra de productes d’una màquina expenedora, tenint en compte l’inventari, el pagament i el canvi.
- 🏧 La màquina expenedora disposa de:
- Una matriu que representa les posicions dels productes. Cada cel·la conté un array amb tres elements:
- El nom del producte (string).
- El preu (nombre).
- La quantitat disponible.
- Un llistat de monedes que conté la màquina expenedora per donar el canvi.
- Una matriu que representa les posicions dels productes. Cada cel·la conté un array amb tres elements:
- 🛒 L’usuari selecciona un producte indicant les coordenades on es troba el producte, per exemple, A1 que representa (0,0) i l’import a pagar.
- 💰 Si el producte existeix i es pot fer efectiva l’operació, la màquina retorna el nom del producte i un array amb el canvi (usant el menor nombre de monedes possible).
- ❌ Si ocorre un error (producte no vàlid, sense estoc, import insuficient o sense canvi), es mostra un missatge i es retorna tot el diners pagat.
💶 La màquina només accepta i entrega canvi en monedes de: 0.01€, 0.05€, 0.10€, 0.20€, 0.50€, 1€ i 2€.
Exercici 63: Calendari xinès
📅 Crea una funció que, donat un any, indiqui l’element i l’animal corresponents del cicle sexagenari del zodíac xinès.
- 🔁 El cicle combina 5 elements: fusta 🌳, foc 🔥, terra ⛰️, metall ⚙️ i aigua 💧.
- I 12 animals: rata 🐀, bou 🐂, tigre 🐅, conill 🐇, drac 🐉, serp 🐍, cavall 🐎, ovella 🐑, mico 🐒, gall 🐓, gos 🐕 i porc 🐖.
- Cada element es repeteix durant dos anys consecutius.
- L’últim cicle va començar el 1984 amb Fusta 🌳 Rata 🐀.
Exercici 64: Els nombres que falten
🔍 Donat un array d’enters ordenat i sense repeticions, crea una funció que retorni els nombres que falten entre el menor i el major de l’array.
Exercici 65: Bubble Sort
📝 Crea un programa que ordeni una llista de nombres enters utilitzant l’algoritme de Bubble Sort.
- 🧮 El programa ha de permetre introduir una llista de nombres desordenats.
- 🔄 Implementa l’algoritme pas a pas per ordenar la llista de menor a major.
- 🖥️ Mostra la llista ordenada al finalitzar.
Exercici 66: Insertion Sort
📝 Crea un programa que ordeni una llista de nombres enters utilitzant l’algoritme de Insertion Sort.
- 🧮 El programa ha de permetre introduir una llista de nombres desordenats.
- 🔄 Implementa l’algoritme pas a pas per ordenar la llista de menor a major.
- 🖥️ Mostra la llista ordenada al finalitzar.
Exercici 67: Quick Sort
📝 Crea un programa que ordeni una llista de nombres enters utilitzant l’algoritme de Quick Sort.
- 🧮 El programa ha de permetre introduir una llista de nombres desordenats.
- 🔄 Implementa l’algoritme Quick Sort per ordenar la llista de menor a major.
- 🖥️ Mostra la llista ordenada al finalitzar.
Exercici 68: Cua de supermercat
🛒 Crea un programa que simuli la cua de clients esperant en un supermercat.
- 👥 Els clients arriben i s’afegeixen al final de la cua (encolar o enqueue).
- 🏪 El caixer atén els clients en ordre, traient-los del davant de la cua (desencolar o dequeue).
- 📊 El programa ha de permetre afegir nous clients i atendre els clients en l’ordre correcte.
- 🔢 Després de cada operació, mostra el nombre de clients que queden a la cua.
- ❗ Controla els casos en què s’intenti atendre un client quan la cua està buida.
- 🔁 La simulació continua fins que l’usuari decideixi finalitzar-la.
Exercici 69: Pila de plats
📝 Crea un programa que simuli la gestió d’una pila de plats en un restaurant.
- 🍽️ Els plats s’apilen un sobre l’altre, per això només es pot treure l’últim plat que es va col·locar (desapilar o pop).
- 🥄 El programa ha de permetre a l’usuari afegir un plat nou a la pila (apilar o push) o treure el plat superior (desapilar).
- 📊 Després de cada acció, mostra quants plats queden a la pila i el seu ordre.
- ❗ Controla els casos en què s’intenti treure un plat quan la pila està buida.
- 🔁 El programa ha de continuar fins que l’usuari decideixi acabar la simulació.
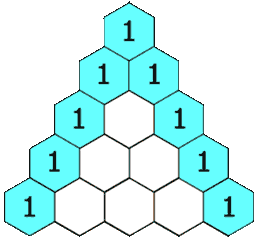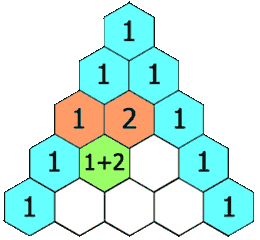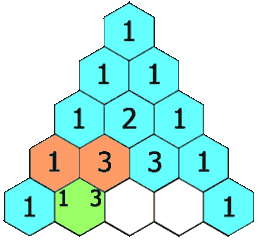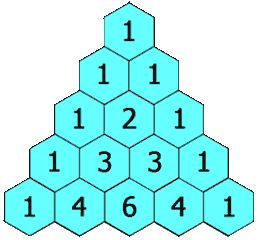
Exercici 70: Triangle de Pascal
🔺 Crea una funció que dibuixi el Triangle de Pascal indicant la mida del costat.
- 🧮 Cada nombre es calcula com la suma dels dos nombres superiors.
- 📊 Mostra el triangle en format text, alineant els nombres correctament.
Exercici 71: Truc o tracte
🎃 Crea un programa especial d’Halloween que interactuï amb els nens i nenes.
- 🕷 L’usuari tria entre “Truc” o “Tracte”.
- 👶 Es introdueix una llista de noms de nens i nenes.
- Si és “Truc” 🎭 🧛♂️ 😈:
- Genera espants aleatoris 🎃 👻 💀 🕷 🕸 🦇.
- Un espant per cada 2 lletres del nom.
- Dos espants si el nom té dues o més “a” o “e”.
- Tres espants si el nom té més de 10 lletres.
- Si és “Tracte” 🧁 🧺 🎒:
- Genera dolços aleatoris 🍬 🍭 🍫 🍪.
- Un dolç per cada 3 lletres del nom.
- Dos dolços si el nom té una o més “i” o “u”.
- Tres dolços si el nom té més de 8 lletres.
📊 Mostra els resultats finals amb els noms i els seus respectius espants o dolços.
Exercici 72: Pou d’aigua
⚙️ Desenvolupa un programa que simuli l’estudi de pous d’aigua i compti quantes unitats poden tenir. Donat un array de nombres enters que representen la quantitat de blocs apilats, calcula quantes unitats d’aigua queden atrapades entre ells.
- 🧱 Cada nombre indica l’alçada de blocs.
- 💧 L’aigua queda atrapada entre blocs més alts.
- 📌 Per exemple, per a l’array
[2, 0, 3, 1, 6, 3, 6], el resultat és6.
| ⏹ | 💧 | ⏹ | ||||
| ⏹ | 💧 | ⏹ | ||||
| ⏹ | 💧 | ⏹ | ||||
| ⏹ | 💧 | ⏹ | ⏹ | ⏹ | ||
| ⏹ | 💧 | ⏹ | 💧 | ⏹ | ⏹ | ⏹ |
| ⏹ | 💧 | ⏹ | ⏹ | ⏹ | ⏹ | ⏹ |
Exercici 73: Generador de contrasenyes
🔐 Crea un generador de contrasenyes configurables que compleixi els següents requisits:
- 🛡️ Longitud entre 8 i 16 caràcters.
- 🔢🔡 Ha d’incloure lletres, números i símbols.
- 🔠 Contenir almenys una lletra majúscula.
- 🔣 Contenir almenys un símbol (per exemple:
#,_,!).
Exercici 74: Generador pseudoaleatori
🎲 Crea un generador de nombres pseudoaleatoris entre 0 i 100 sense fer servir funcions predeterminades de random.
🧠 Has de cercar i implementar una estratègia alternativa com l’algorisme de congruència lineal o alguna fórmula matemàtica creativa.
Exercici 75: Àbac
🧮 Crea un programa capaç de representar un número en àbac.
- 📊 El número es representarà en una matriu 10 x 10.
- 🔢 Cada fila, començant de dalt a baix, representarà les unitats, desenes, centenes, milers, etc.
- 🏛️ Cada columna representarà un dígit del número.
- 📥 El número a representar ha d’estar entre
0i9.999.999.999. - ❗ Si el número és vàlid, es mostrarà l’àbac corresponent.
- ❌ Si el número és invàlid, es mostrarà un missatge d’error.
📌 Per exemple, el número 1234 es representaria així:
| ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― | ⬤ || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― | ⬤ | ⬤ || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― | ⬤ | ⬤ | ⬤ || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― | ⬤ | ⬤ | ⬤ | ⬤ || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― || ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ― |4.4. Dificultat alta 🚨
En aquest nivell, els exercicis plantegen problemes complexos que poden involucrar estructures anidades, algoritmes més elaborats i gestió de casos límit. S’espera que l’alumne sigui capaç de dissenyar solucions integrals, aplicar tècniques avançades i reflexionar críticament sobre l’eficiència i robustesa del codi.
Exercici 76: Avaluador d’expressions matemàtiques
🧮 Crea un programa que rebi una expressió matemàtica escrita com a cadena i calculi el seu resultat respectant l’ordre d’operacions.
- 🔢 L’expressió pot incloure nombres enters, parèntesis i els operadors
+,-,*i/. - 💬 El programa ha d’analitzar la cadena, validar la seva sintaxi i calcular el resultat correcte.
- 🧾 S’ha de respectar la jerarquia d’operadors (PEMDAS): primer parèntesis, després multiplicacions/divisions, i finalment sumes/restes.
- ❗ El programa ha d’avaluar correctament expressions anidades com:
“(2 + 3) * (7 - 2) / (1 + 1)” → 12.5 - ❌ Si l’expressió és invàlida, es mostrarà un missatge d’error adequat.
Exercici 77: Fibonacci
🌀 Escriu un programa que imprimeixi els 50 primers nombres de la successió de Fibonacci començant en 0.
- 📖 La sèrie Fibonacci és una successió on cada nombre és la suma dels dos anteriors:
0, 1, 1, 2, 3, 5, 8, 13...
Exercici 78: Factorial recursiu
📈 Crea un programa que calculi el factorial d’un nombre enter no negatiu utilitzant una funció recursiva.
- ✍️ El programa ha de sol·licitar a l’usuari un nombre enter major o igual a 0.
- ↪️ La funció es definirà així:
factorial(n) = n * factorial(n - 1)
amb el cas base:factorial(0) = 1 - 🖥️ Mostra el resultat per pantalla.
- ⚠️ Si el nombre és negatiu, mostra un missatge d’error.
Exercici 79: Calcular dies entre dates
📅 Crea una funció que calculi i retorni quants dies hi ha entre dues dates, donades en format text.
- 🗓️ El format d’entrada serà
"dd/MM/yyyy". - 🔄 La diferència es calcularà de manera absoluta (sense importar l’ordre de les dates).
- ❗ Si alguna cadena no representa una data vàlida, s’ha de mostrar un missatge d’advertència.
Exercici 80: Joc de tres en ratlla
🕹️ Crea una funció que analitzi una matriu 3x3 composta per "X" i "O", i retorni:
"X"si van guanyar les ❌."O"si van guanyar les ⭕."Empat"si ningú no va guanyar."Nul"si la matriu és invàlida (proporció incorrecta o van guanyar ambdós).
⚠️ Nota: la matriu pot tenir cel·les buides representades per "".
Exercici 81: Joc Sudoku
🧩 Crea un programa que permeti jugar al clàssic joc de Sudoku sobre un tauler de 9x9.
- 📐 El tauler es representarà com una matriu bidimensional d’enters.
- 🔲 Cada cel·la pot contenir un número de l’1 al 9 o estar buida (representada per
0o un espai). - 🗂️ El tauler es divideix en 9 subquadres de 3x3.
- 🎲 En iniciar el joc, el programa ha d’omplir entre 25 i 30 números inicials, distribuïts per tot el tauler.
- ❗ Com a restricció, ha d’haver-hi exactament dues subquadres amb un sol número inicial. Les altres poden contenir entre 2 i 5 números, però cap no ha de superar els 5.
- 👤 Un cop inicialitzat el tauler, el programa sol·licitarà a l’usuari que introdueixi els valors un a un, indicant la fila, la columna i el número desitjat.
- ✅ Abans de col·locar el número, s’ha de verificar que no estigui repetit a la mateixa fila ni a la mateixa columna.
- 🔄 Després de cada intent, es mostrarà el tauler actualitzat amb els números introduïts.
- ❌ Qualsevol error en la introducció de dades (número fora de rang, cel·la ocupada, etc.) ha de ser notificat a l’usuari.
- 🏁 El programa finalitzarà quan l’usuari completi correctament el tauler. Al final, mostrarà el tauler final i el nombre total d’intents realitzats.
Exercici 82: Joc batalla naval (versió contra la màquina)
⚓ Crea un programa que permeti jugar al clàssic joc Batalla naval contra la màquina.
- 🗺️ El tauler serà una matriu bidimensional de mida 10x10 (fila x columna).

- 🤖 La màquina col·locarà de forma aleatòria els vaixells, que poden ser verticals, horitzontals o diagonals. No poden haver-hi dos o més vaixells que utilitzin la mateixa cel·la.
- 🚢 La quantitat de vaixells serà:
- 1 cuirassat de 4 cel·les
- 2 creuers de 3 cel·les cadascun.
- 3 destructors de 2 cel·les cadascun.
- 4 submarins d’1 cel·la cadascun.
- 🎯 El jugador intentarà enfonsar els vaixells introduint coordenades (fila i columna).
- 💥 Després de cada intent, el programa ha d’indicar si ha estat un “impacte” o “aigua” (fallada).
- ⏳ Hi haurà un límit d’intents totals per enfonsar tots els vaixells.
- 📊 Per cada iteració, el programa mostrarà el tauler actualitzat, indicant les posicions ja atacades i els encerts. La quantitat màxima d’intents i els realitzats.
- 🏁 El joc acaba si:
- ✅ El jugador enfonsa tots els vaixells (Guanya)
- ❌ S’arriba al nombre màxim d’intents (Perd).
- 📈 Al finalitzar, el programa mostrarà el nombre total d’intents realitzats en la partida.
❗ Important: El jugador no té la funcionalitat de col·locar vaixells; només ha d’intentar enfonsar els vaixells col·locats aleatòriament per la màquina. La màquina no ataca al jugador. Pots representar el tauler amb caràcters o símbols per mostrar aigua, impactes i posicions no atacades.
Exercici 83: Torre de Hanoi (versió recursiva)
🏰 Crea un programa que resolgui el clàssic problema de la Torre de Hanoi utilitzant recursivitat.
- 🗼 El joc consisteix en tres torres (
A,BiC) i un nombre variable de discs (entre 3 i 8) apilats a la torre A, ordenats de més gran a més petit de baix cap amunt. - 🎯 L’objectiu és traslladar tots els discs des de la torre A fins a la torre C, complint les següents regles:
- 🔄 Només es pot moure un disc alhora.
- 📏 Només es pot col·locar un disc sobre un altre si és més petit.
- 🗺️ Els discs només es poden moure d’una torre a una altra (A, B, C).
- 📥 El programa ha de demanar a l’usuari el nombre de discs a resoldre.
- 📜 Ha de mostrar pas a pas cada moviment necessari per completar la solució.
- ↪️ Utilitza una funció recursiva per resoldre el problema.
Per exemple, el programa ha d’indicar a la pantalla instruccions com:
Mou disc 1 (Petit) de A a CMou disc 2 (Mitjà) de A a BMou disc 1 (Petit) de C a BMou disc 3 (Gran) de A a C...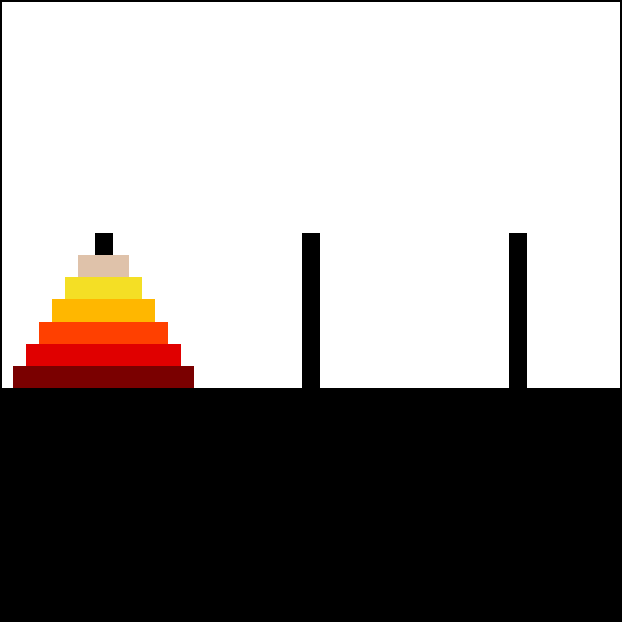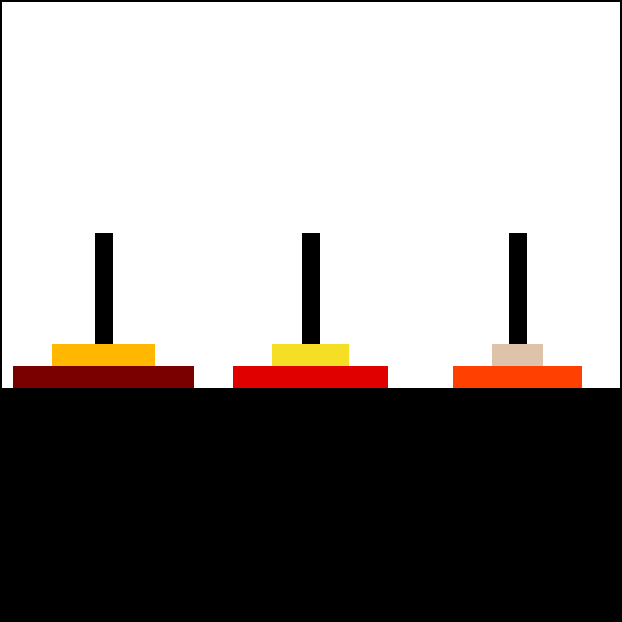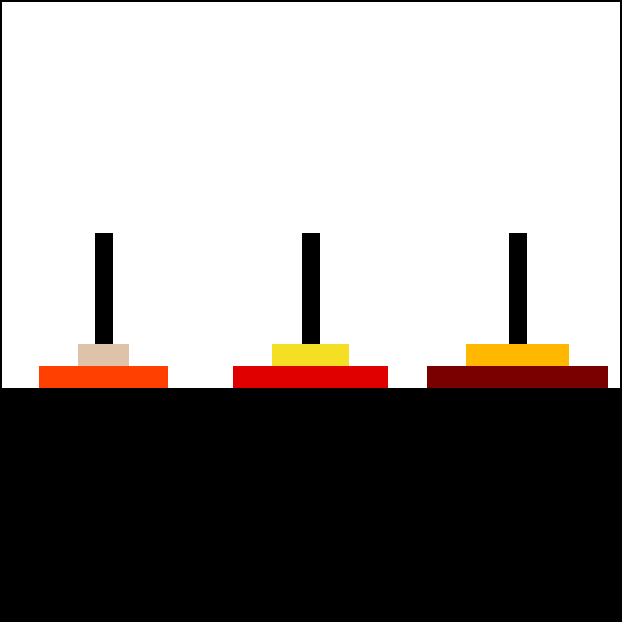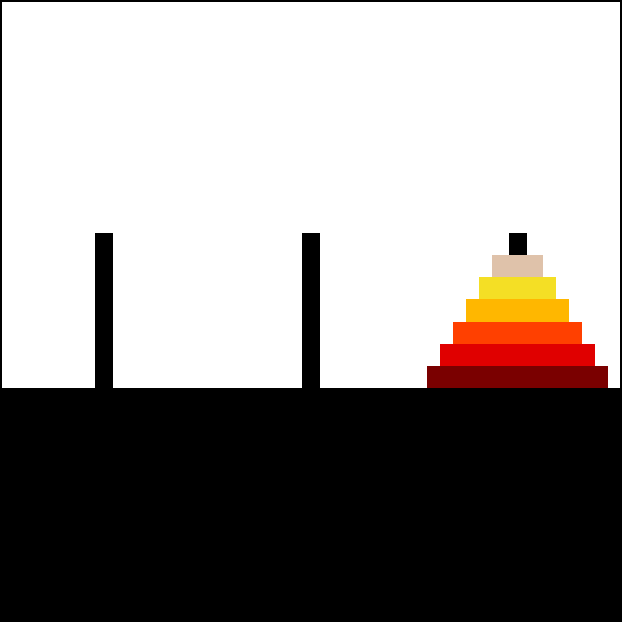
Exercici 84: El problema de les N reines
👑 Crea un programa que resolgui el clàssic problema de les N reines utilitzant l’algoritme de backtracking.
- 📏 L’objectiu és col·locar N reines en un tauler de NxN sense que cap s’atacqui entre elles.
- 🚫 Les reines no poden compartir la mateixa fila, columna ni diagonal.
- 🖥️ El programa ha de mostrar una solució vàlida (o totes si es desitja) indicant les posicions al tauler.
- 🔄 Utilitza backtracking per explorar les possibles combinacions i retrocedir quan una col·locació no és vàlida.
- 📐 L’usuari pot indicar la mida N del tauler (per exemple, 4 o 8).

👉 Més informació: Backtracking - Wikipedia.
Exercici 85: Escapa del laberint
🧭 Crea un programa que trobi un camí des de l’entrada fins a la sortida en un laberint representat com una matriu d’1s (pas) i 0s (paret).
- 🗺️ El laberint es representa amb una matriu NxM d’enters.
- 🚪 L’entrada està a l’angle superior esquerre (0, 0) i la sortida a l’angle inferior dret (N-1, M-1).
- 📥 El laberint s’inicialitza manualment com una matriu fixa, afegint 1s de forma contigua fins a la sortida. Per exemple:
laberint = [[1, 1, 1, 1],[1, 1, 0, 1],[0, 1, 1, 0],[1, 0, 1, 1]]
- 🎯 El programa ha de trobar una ruta possible des de l’entrada fins a la sortida, avançant en les quatre direccions (amunt, avall, esquerra, dreta), sense travessar parets.
- 🔄 Explora camins possibles i retrocedeix si s’arriba a un carreró sense sortida.
- 📊 Mostra el camí trobat sobre el tauler (per exemple, amb ”*” o amb coordenades).
- 🔚 És possible que el laberint tingui múltiples solucions, per això s’ha de mostrar el camí més curt.
❗ Important: Es contempla que el laberint sempre ha de tenir un camí vàlid des de l’entrada fins a la sortida. No s’han de considerar laberints sense solució.
Exercici 86: Algoritme genètic per trobar una paraula
🧬 Crea un programa que utilitzi un algoritme genètic per “evolucionar” una cadena de text aleatòria fins que coincideixi amb una paraula objectiu.
Què ha de fer el programa?
- 📝 L’usuari introdueix una paraula objectiu, per exemple:
"hola". - 🎲 El programa genera una població inicial de cadenes aleatòries de la mateixa mida que la paraula objectiu.
- 📊 A cada generació, s’avalua cada cadena amb una funció de fitness, que mesura com de semblant és a la paraula objectiu (per exemple, quantes lletres coincideixen en la posició correcta).
- 👪 S seleccionen les cadenes més aptes per a reproduir-se (selecció de pares).
- 🔄 Es realitza un creuament (crossover) entre pares per crear nous fills.
- 🎯 A cada nou fill se li pot aplicar una mutació aleatòria (canviar una lletra a l’atzar).
- 🔁 Aquest procés es repeteix generació rere generació fins que:
- es troba la paraula exacta, o
- s’assoleix un nombre màxim de generacions.
Has d’implementar:
- ✅ Una funció de fitness que calcula un nombre que representa com de “bona” és una cadena. Per exemple:
Objectiu: HOLACadena: HAZAFitness: 3 lletres coincideixen (H, A, A)
- 🔍 Selecció de pares. Pots usar per exemple els 10 millors individus de la població.
- 🔗 Creuament (crossover). Combinar dues cadenes, usant per exemple meitat i meitat.
- 🎲 Mutació aleatòria: canvia una lletra a l’atzar en una cadena amb certa probabilitat.
📈 Mostra l’evolució de les generacions i el nombre de passos necessaris per arribar al resultat.
