Pseudocódi
Introducció a l’ús del pseudocodi com a eina per al disseny i la planificació d’algoritmes, abans d’escriure programes en un llenguatge concret.
Coneixements previs
Referències
- Cambridge International - Pseudocode Guide for Teachers (PDF)
- Wikipedia - Pseudocode
- Joyanes Aguilar, L. (2020). Fundamentos de programación. McGraw-Hill. ISBN: 978-607-15-1468-4.
Índex
- Què és el pseudocodi?
- Operadors i paraules reservades
- Tipus de dades
- Variables i constants
- Estructures de control
5.1. Seqüencial
5.2. Alternativa
5.3. Iterativa - Estructures modulars
6.1. Procediments
6.2. Funcions
6.3. Pas de paràmetres
6.4. Funcions predefinides - Estructures de dades complexes
7.1. Vectors i Arrays
7.2. Matrius - Recursivitat
- Operacions d’entrada i sortida de dades
- Eines per treballar amb pseudocodi
- Exercicis
1. Què és el pseudocodi?
El pseudocodi és una eina molt útil per dissenyar i entendre algorismes abans de traduir-los a un llenguatge de programació específic. Es tracta d’un llenguatge semblant al llenguatge natural, que facilita l’escriptura d’instruccions de manera clara i senzilla per a qualsevol programador, independentment del llenguatge que utilitzi després.
El pseudocodi no és un llenguatge de programació per si mateix, sinó un sistema que utilitza expressions limitades per representar les estructures bàsiques de control, que vam veure en els paradigmes de programació.
Quan escrivim pseudocodi, busquem expressar algorismes que tinguin una solució finita, amb un únic punt d’inici. Aquesta forma d’estructurar els algorismes ens ajuda molt a l’hora de traduir-los posteriorment a un llenguatge de programació real.
2. Operadors i paraules reservades
Tot i que no existeix una norma estricta per escriure pseudocodi, és recomanable seguir certes convencions que facilitin la seva posterior traducció a codi d’un llenguatge de programació.
Operadors:
Són símbols o paraules clau que s’utilitzen en els llenguatges per realitzar operacions sobre un o més valors (anomenats operands). Aquestes operacions poden ser matemàtiques, lògiques, de comparació, entre d’altres.
| Tipus | Operadors |
|---|---|
| Aritmètics | + - * / Div Mod ^ |
| Relacionals | = < <= > >= <> |
| Lògics | and or not |
| Assignació | ← |
| Comentaris | // |
Paraules reservades:
Són paraules pròpies del llenguatge que tenen un significat especial i un ús específic. No es poden utilitzar literalment com a noms de variables, funcions o altres identificadors perquè estan reservades per controlar l’estructura i el funcionament del programa.
| Català | Anglès | Descripció |
|---|---|---|
| Inici | Start | Marca l’inici de l’algorisme o programa. |
| Fi | End | Indica el final de l’algorisme o programa. |
| Si | If | Condicional que executa un bloc si la condició és verdadera. |
| Llavors | Then | Indica l’acció a fer quan la condició del “Si” és verdadera. |
| Sinó | Else | Bloc alternatiu que s’executa si la condició del “Si” és falsa. |
| Altrament | Otherwise | Alternativa per a condicions addicionals o per defecte. |
| Per a | For | Bucle que es repeteix un nombre determinat de vegades. |
| Dins de | In | Usat per indicar el conjunt o rang en bucles o condicions. |
| Mentre | While | Bucle que es repeteix mentre la condició sigui verdadera. |
| Fer | Do | Inici del bloc que s’executa dins d’un bucle o condicional. |
| Repetir | Repeat | Bucle que s’executa almenys una vegada fins que es compleixi una condició. |
| Fins que | Until | Condició que indica fins quan ha de continuar un bucle. |
| Segons | Switch | Estructura de selecció múltiple basada en valors específics. |
| Cas | Case | Cada opció dins d’una estructura “Segons” (switch). |
| Procediment | Procedure | Subrutina que executa una sèrie d’instruccions sense retornar valor. |
| Funció | Function | Subrutina que executa instruccions i retorna un valor. |
| Llegir | Read | Captura dades introduïdes per l’usuari o des d’una font externa. |
| Escriure | Write | Envia informació a la pantalla, a un fitxer o a altres dispositius. |
| Imprimir | Mostra informació per pantalla o sortida estàndard. | |
| Retornar | Return | Retorna un valor des d’una funció o n’interromp l’execució. |
| Incrementar | Increment | Augmenta el valor d’una variable (normalment en bucles). |
| Cadascun | Each | Indica una iteració sobre cada element d’una col·lecció o conjunt. |
| Per valor | By Value | Es passa una còpia del valor original al paràmetre del procediment o funció. |
| Per referència | By Reference | Es passa l’adreça de memòria de la variable original al paràmetre del procediment o funció. |
3. Tipus de dades
Els tipus de dada determinen la naturalesa de la informació, com s’emmagatzema a la memòria i quines operacions es poden realitzar sobre ella. Normalment s’utilitza per determinar una variable o constant.
| Català | Anglès | Descripció |
|---|---|---|
| Caràcter | Char | Un sol símbol o lletra. |
| Cadena | String | Seqüència de caràcters. |
| Enter | Integer | Nombre enter sense part decimal. |
| Decimal | Real | Nombre amb part decimal (general). |
| Booleà | Boolean | Valor cert o fals. |
| Data | Date | Representa dates i hores. |
Els tipus de dades que es mostren són els més comuns i reconeguts en general, però és possible trobar altres tipus o subtipus que representin diferents conjunts o subconjunts de dades, segons el llenguatge de programació o el context d’ús.
4. Variables i constants
Les variables són etiquetes o noms que representen llocs a la memòria on es guarden valors temporals. Aquestes permeten emmagatzemar, modificar i manipular dades durant l’execució de l’algorisme, simulant la lògica del programa sense necessitat d’entrar en detalls tècnics específics.
Per declarar una variable, fem servir l’estructura següent:
Inici Definir numero1 com Enter;FiAquí, Enter és el tipus de dada i numero1 el nom de la variable, que serveix per referenciar-la.
Les variables poden canviar de valor mitjançant una operació anomenada assignació, que reemplaça el valor anterior per un de nou. Per exemple:
Inici Definir numero1 com Enter; numero1 ← 5; // Es canvia el valor de 5 per 10 a la variable numero1 numero1 ← 10;FiD’altra banda, les constants són valors fixos que no canvien durant l’execució del programa. Solen nomenar-se amb lletres majúscules per fer-les més visibles i facilitar-ne la comprensió. La declaració és similar a la de les variables, però només s’assigna un valor una vegada, que no podrà modificar-se després.
Exemple de constants:
Inici Definir PI com Real; PI ← 3,14159; Definir LIMIT_MAXIM com Enter; LIMIT_MAXIM ← 500;Fi5. Estructures de control
Les estructures de control permeten definir el flux d’execució d’un algorisme. En pseudocodi, aquestes estructures segueixen l’estil de la programació estructurada, dividint el programa en blocs lògics. Podem classificar-les en tres grans grups: seqüencial, alternativa i iterativa.
5.1. Seqüencial
Les instruccions s’executen en l’ordre en què apareixen, una darrere l’altra. No hi ha decisions ni repeticions: simplement, el programa segueix un camí lineal, de dalt a baix.
Inici <instrucció1> ... <instruccióN>Fi5.2. Alternativa
Aquestes estructures permeten que l’algorisme prengui decisions. Segons una condició, s’executarà una part del codi o una altra.
1. Alternativa simple (If)
S’executa un bloc d’instruccions només si es compleix una condició booleana.
Si <condició> Llavors <instruccions>Fi Si2. Alternativa doble (If-Else)
Permet executar un bloc o un altre, segons es compleixi o no la condició.
Si <condició> Llavors <instruccions1>Si no <instruccions2>Fi Si3. Alternativa múltiple (Switch)
Permet avaluar una expressió contra múltiples casos possibles.
Segons <expressió> Fer Cas <valor1> <instruccions1> Cas <valor2> <instruccions2> ... Un altre cas <instruccionsN>Fi SegonsAquesta estructura també es pot implementar anidant diverses estructures Si - Si no.
Si <condició1> Llavors <instruccions1>Si no Si <condició2> Llavors <instruccions2> Si no Si <condició3> Llavors <instruccions3> Si no <instruccions4> Fi Si Fi SiFi Si5.3. Iterativa
Aquestes estructures permeten repetir un bloc d’instruccions mentre es compleixi una condició o durant un nombre de vegades determinat.
1. Iteració amb sortida al principi (While)
Primer s’avalua la condició. Si és vertadera, s’executen les instruccions. Si no, es surt del bucle.
Mentrestant <condició> Fer <instruccions>Fi Mentrestant2. Iteració amb sortida al final (Do-While)
Primer s’executen les instruccions i després es comprova la condició.
Fer <instruccions>Mentrestant <condició>Aquesta estructura també es pot trobat amb Repeat. Es lo mateix.
Repetir <instruccions>Fins Que <condició>3. Iteració amb comptador (For)
Utilitza una variable de control que s’incrementa o decrementa fins a assolir un límit.
Amb increment positiu:
Definir i com Enter;Per a i ← 1 Fins N Amb pas Increment 1 Fer <instruccions>Fi Per aAmb increment negatiu:
Definir i Com Enter;Per a i ← N Fins 1 Amb pas Increment -1 Fer <instruccions>Fi Per a4. Iteració per a cada element (For Each)
Recorre tots els elements d’un conjunt.
Definir conjunt[N] Com Entero;Per a Cada element En conjunt Fer <instruccions>Fi Per a CadaL’ús d’aquest tipus d’estructura requereix conèixer els tipus de dades complexes, que s’expliquen en el següent apartat: Vectors i Arrays
6. Estructures modulars
En programació, descompondre un problema en parts més petites i manejables és fonamental per millorar l’organització, reutilització i llegibilitat del codi. Una de les formes més comunes de fer-ho és mitjançant estructures modulars, com els procediments i funcions.
Podem utilitzar pseudocodi per representar de manera senzilla aquesta descomposició modular, sense necessitat d’utilitzar un llenguatge de programació específic.
6.1. Procediments
Un procediment és un bloc d’instruccions independent que rep un nom (Per convenció, s’acostuma a utilitzar un verb en infinitiu, i la primera lletra s’escriu en majúscula per indicar l’acció que realitza) i s’executa quan és invocat des d’un altre bloc de codi o des d’un altre programa.
A més, pot rebre un o més paràmetres d’entrada (també anomenats arguments), que són variables acompanyades del seu tipus de dada. Aquests paràmetres permeten al procediment treballar amb informació concreta, adaptant el seu comportament als valors rebuts. És important tenir en compte que no és obligatori definir paràmetres. Si el procediment no necessita rebre informació, es pot indicar el seu nom seguit de parèntesis buits.
Un cop invocat, el procediment executa totes les instruccions definides en el seu interior fins arribar al final del bloc. Després, retorna el control al programa o bloc que l’ha cridat, però no retorna cap valor com a sortida.
Sintaxi general
Procediment nom (paràmetre1 tipus, paràmetre2 tipus, …) <instruccions>Fi Procediment- Exemple 1: Procediment sense paràmetres
En aquest exemple, es defineix un procediment que no rep arguments. Per tant, en la seva crida s’indicarà únicament el nom seguit de parèntesis buits.
Procediment MostrarMissatge() Escriure "Aquest es un missatge";Fi Procediment
Inici MostrarMissatge()Fi- Exemple 2: Procediment amb paràmetre
Utilitzant el mateix exemple anterior, s’afegeix un paràmetre al procediment per mostrar una informació.
Procediment MostrarMissatge(missatge Cadena) Escriure "El paràmetre rebut es: ", missatge;Fi Procediment
Inici Definir salutacio Com Cadena; salutacio ← "Hola"; MostrarMissatge(salutacio);Fi6.2. Funcions
Una funció és similar a un procediment, amb la diferència que sempre retorna un valor com a resultat de la seva execució. També pot rebre paràmetres d’entrada.
Sintaxi general
Funció nom (paràmetre1 tipus, paràmetre2 tipus, …) : tipusRetorn <instruccions> ... Retornar valor;Fi FuncióExemple: Funció que suma dos números
Funció Sumar(a Enter, b Enter) : Enter Definir resultat com Enter; resultat ← a + b; Retornar resultat;Fi Funció
Inici Definir x, y, suma Com Enter; Imprimir "Introdueix el primer número:"; Llegir x; Imprimir "Introdueix el segon número:"; Llegir y; suma ← Sumar(x, y); Imprimir "El resultat és: ", suma;Fi6.3. Pas de paràmetres
Tant en els procediments com en les funcions és possible enviar paràmetres, que són valors o variables que s’utilitzen dins el cos del bloc.
Els paràmetres permeten que un procediment o funció treballi amb dades externes, adaptant el seu comportament en funció dels valors que rep. D’aquesta manera, s’evita escriure el mateix codi diverses vegades, reutilitzant el bloc amb diferents dades.
Depenent de com s’enviïn les dades al procediment o funció, els paràmetres poden comportar-se de dues maneres:
- Pas del paràmetre per valor
En el pas per valor, al procediment o funció se li envia una còpia de la dada original. Això significa que qualsevol canvi que es faci sobre el paràmetre no afecta el valor original de la variable en el programa principal.
Procediment Incrementar(x Enter per Valor) x ← x + 1;Fi Procediment
Inici Definir x Com Enter; x ← 5; Escriure x; Incrementar(x); Escriure x;FiEn executar l’exemple, veiem que el valor de x continua sent el mateix.
55- Pas del paràmetre per referència
En el pas per referència, al procediment o funció se li envia l’adreça de memòria de la variable original. Això implica que qualsevol canvi sobre el paràmetre modificarà directament el valor de la variable original.
Procediment Incrementar(x Enter Enter per Referència) x ← x + 1;Fi Procediment
Inici Definir x Com Enter; x ← 5; Escriure x; Incrementar(x); Escriure x;FiEn executar l’exemple, no passarà com en l’anterior; aquesta vegada x tindrà un valor diferent un cop cridat el procediment.
56Quan utilitzar una forma o una altra?
- S’utilitzarà per valor quan volem protegir la dada original i evitar modificacions. És útil si només necessitem llegir o treballar temporalment amb la dada.
- S’utilitzarà per referència quan necessitem que el procediment o funció modifiqui el valor de la variable original. És útil, per exemple, per retornar resultats o actualitzar valors.
6.4. Funcions predefinides
En pseudocodi, igual que a la majoria de llenguatges de programació, existeixen funcions predefinides que ens permeten realitzar operacions comunes sense necessitat d’escriure tot el procediment des de zero.
Aquestes funcions estan ja integrades a la gran majoria de llenguatges i ens permeten treballar amb nombres, cadenes de text i operacions lògiques de forma més ràpida i senzilla. Fer-ne un bon ús ens ajuda a escriure algoritmes més clars i no haver de desenvolupar des de zero aquestes operacions.
A continuació es mostren algunes funcions predefinides:
Són funcions que permeten realitzar operacions numèriques avançades.
Arrel(n)→ Retorna l’arrel quadrada den.Potencia(base, exponent)→ Calcula la potència d’un nombre.Abs(n)→ Retorna el valor absolut den.Arrodonir(n)→ Arrodoneix el nombrena l’enter més proper.Aleatori(inf, sup)→ Retorna un nombre aleatori entre els valors indicats.
Aquestes funcions ens permeten treballar amb textos o paraules (també anomenades cadenes de caràcters).
Longitud(cadena)→ Retorna quants caràcters té la cadena.SubCadena(cadena, inici, fi)→ Extreu una part de la cadena.Concatenar(cad1, cad2)→ Uneix dues cadenes en una sola.Majúscules(cadena)iMinúscules(cadena)→ Converteix tot el text a majúscules o minúscules.
7. Estructures de dades complexes
A més dels tipus de dades simples com enters, reals o cadenes, existeixen estructures de dades complexes que ens permeten emmagatzemar i gestionar col·leccions de valors relacionats. Les dues estructures més comunes són els vectors i les matrius.
Amb el coneixement que tenim fins ara, si volem guardar a memòria el nom d’una fruita, creem una variable. Però, què passa si ara volem guardar una llista de fruites, per exemple, 100 fruites? Hauríem de crear 100 variables diferents? Això seria inviable i poc pràctic.
Per això, existeixen estructures de dades que faciliten l’emmagatzematge ordenat de múltiples dades relacionades i permeten la seva manipulació mitjançant índexs. Aquestes estructures ens ajuden a gestionar col·leccions de dades de forma eficient i organitzada.
7.1. Vectors i Arrays
Un vector o array son termes que serveixen per representar un conjunt d’elements del mateix tipus emmagatzemats en una sola dimensió, és a dir, una llista ordenada. Cada element s’accedeix mitjançant un índex, que indica la seva posició dins del vector.
Declaració
La seva sintaxi és similar a la d’una variable però ara s’indica entre [ ] la quantitat numèrica d’elements. Cal tenir en compte que tots els elements han de ser del mateix tipus. No és possible tenir un vector amb diferents tipus de dades.
Definir numeros[5] Com Enter;// Vector amb 5 elementsAccés i recorregut
Per accedir als elements d’un vector, s’utilitza un índex, que representa la posició de l’element dins del mateix. En aquest cas, l’índex començarà en 1, i cada posició s’identifica pel seu número d’ordre.
L’índex mai no ha de superar el límit establert en la declaració del vector. Per exemple, si s’ha declarat un vector amb 5 elements, no és vàlid accedir a l’índex 6 o superior, ja que s’estaria intentant accedir a una posició que no existeix en memòria.
numero[2] ← 7; // S’afegeix el valor 7 a la posició 2
Escriure "El valor a la posició 2 és: ", numero[2];Per recórrer els registres dels vectors s’emprarà un bucle.
// Afegir valors als elements del vectorPer i ← 1 Fins 5 Fer Escriure "Introdueix el número ", i, ":" ; Llegir numeros[i];Fi Per
// Llegir els valors dels elements del vectorPer i ← 1 Fins 5 Fer Escriure "El número a la posició ", i, " és: ", numeros[i];Fi Per7.2. Matrius
Una matriu és una estructura bidimensional que emmagatzema dades en files i columnes. És útil per representar taules, mapes, imatges o qualsevol tipus d’informació que necessiti un doble índex per al seu accés. Una manera senzilla d’entendre-ho és pensar en el taulell del joc Hundir la flota, on cada casella es localitza amb una coordenada composta per una fila i una columna. Així funciona una matriu.
Declaració
Definir matriu[3,4] Com Real; // Matriu de 3 files i 4 columnesDefinir taulell[10,10] Com Enter; // Matriu de 10 files i 10 columnesAccés i recorregut
S’accedeix a cada element amb dos índexs: fila i columna.
matriu[1,1] ← 4.5; // S’afegeix el valor 4.5 a la posició 1,1
Escriure "El valor a la posició 1,1 és: ", matriu[1,1];Per recórrer les files i columnes de la matriu s’empraran dos bucles anidats.
// Afegir valors a la matriuPer i ← 1 Fins 3 Fer Per j ← 1 Fins 4 Fer Escriure "Introdueix el valor per la posició (", i, ",", j, "):" ; Llegir matriu[i,j]; Fi PerFi Per
// Mostrar els valors de la matriuPer i ← 1 Fins 3 Fer Per j ← 1 Fins 4 Fer Escriure "El valor a (", i, ",", j, ") és: ", matriu[i,j]; Fi PerFi Per8. Recursivitat
La recursivitat és una tècnica de programació en la qual una funció (o procediment) es crida a si mateixa per resoldre un problema. És especialment útil quan el problema es pot dividir en subproblemes del mateix tipus, més petits.
Encara que pot semblar complexa al principi, la recursivitat permet crear solucions elegants i molt potents. No obstant això, és important usar-la amb cura per evitar errors com crides infinites o consum excessiu de memòria.
Una funció recursiva té dues parts fonamentals:
- Cas base: la condició que atura la recursió.
- Crida recursiva: la funció es crida a si mateixa amb un nou valor, acostant-se al cas base.
A continuació es mostrarà un exemple d’un comptador cap enrere, que imprimeix nombres des de n fins a 1. Per entendre-ho millor, es presentaran dues versions: una iterativa i una altra recursiva.
- Forma iterativa:
Funcion ComptadorCapEnrere(n: Enter) Per i ← n Fins 1 Amb pas Paso -1 Fer Escriure i; Fi PerFi Funcion
Inici ComptadorCapEnrere(5);Fi- Forma recursiva
Funcion ComptadorCapEnrere(n: Enter) Si n > 0 Llavors // cas base Escriure n; ComptadorCapEnrere(n - 1); // crida recursiva Fi SiFi Funcion
Inici ComptadorCapEnrere(5); // Crida inicialFiEn la gran majoria de casos, un problema es pot resoldre tant de forma iterativa com recursiva. No obstant això, la recursivitat pot resultar més intuïtiva i senzilla d’aplicar en certs contextos, especialment en problemes amb estructura jeràrquica o que poden dividir-se naturalment en subproblemes.
Exemples clàssics on la recursivitat destaca per la seva claredat són el càlcul del factorial, la sèrie de Fibonacci o el recorregut d’estructures de dades com arbres i grafos. Aquests problemes, tot i que també es poden resoldre de forma iterativa, solen tornar-se molt més complexos d’implementar sense recursió. En canvi, la recursivitat permet expressar la solució de manera més directa, llegible i elegant.
-
🔁 El problema es pot dividir en subproblemes del mateix tipus.
Per exemple, per calcular el factorial d’un númeron, n’hi ha prou de multiplicarnpel factorial den - 1, que és el mateix tipus d’operació a una escala menor. -
❓ El nombre de passos no és fix o no es coneix d’antuvi.
En problemes com el recorregut d’un arbre binari o la cerca de solucions en un laberint, la profunditat del procés depèn de les dades i no es pot predir fàcilment. -
🔍 La solució iterativa és molt més complexa o menys clara.
Alguns algoritmes, com els de recorregut en profunditat (DFS) o certs algoritmes de generació de combinacions o particions, són significativament més senzills d’expressar amb recursivitat. -
📐 Existeix una definició matemàtica recursiva.
Quan el propi problema ja està formulat de manera recursiva (com Fibonacci o Torres de Hanoi), implementar-lo recursivament sol ser més directe i natural.
Encara que la recursivitat pot ser una eina molt poderosa, no sempre és la millor opció. Té algunes limitacions importants que cal conèixer:
-
Més ús de memòria:
Cada crida recursiva s’emmagatzema a la pila d’execució del programa. Si es fan massa crides (per exemple, en una recursió profunda sense optimització), pot provocar un error de desbordament de pila (stack overflow). -
Possibilitat de recursió infinita:
Si no es defineix correctament un cas base, o si les crides no s’acosten a aquest cas, la funció mai no acaba i s’executa indefinidament. -
Rendiment lent en alguns casos:
Algunes funcions recursives, com la versió clàssica de Fibonacci, recalculen moltes vegades els mateixos valors, cosa que les fa ineficients si no s’apliquen tècniques com la memorització o la programació dinàmica. -
Més dificultat per depurar i trobar errors:
El seguiment d’errors pot ser més complicat en funcions recursives, ja que hi ha moltes crides apilades i el flux del programa no és tan lineal com en una versió iterativa.
9. Operacions d’entrada i sortida de dades
Una de les habilitats fonamentals a l’hora de començar a programar és aprendre com interactuar amb l’usuari, ja sigui per demanar dades o per mostrar resultats. Aquestes accions es coneixen com operacions d’entrada i sortida de dades.
Entrada de dades
L’entrada de dades permet que l’usuari proporcioni informació al programa. En pseudocodi, la instrucció més habitual per a això és:
Llegir(oLlegir nomVariable)
Aquesta instrucció pausa l’execució de l’algorisme i espera que l’usuari introdueixi un valor, que es guarda a la variable indicada.
Algorisme EntradaExemple Definir edad Com Enter; Escriure "Introdueix la teva edad:" Llegir edad;Fi AlgorismeEn aquest exemple, el programa demana a l’usuari la seva edat i la guarda a la variable edad.
Sortida de dades
La sortida de dades permet mostrar informació a l’usuari, enviar-la a un fitxer o a altres dispositius. La instrucció utilitzada per a això és:
Escribir(oEscribir expresión)
Pots mostrar text, el valor d’una variable o el resultat d’una operació.
Algorisme SortidaExemple Definir nom Com Cadena; nom ← "Lucía" Escriure "Benvingut/da, ", nom;Fi AlgorismeAquest exemple mostra una salutació personalitzada, unint un text fix amb el contingut d’una variable.
En alguns contextos, és possible trobar una instrucció específica per mostrar informació per pantalla, normalment utilitzant la paraula clau Imprimir.
Això no significa que s’enviï un document a la impressora, sinó que les dades indicades es visualitzaran a la pantalla, generalment a la consola o sortida estàndard del programa.
El més habitual és que entrada i sortida s’utilitzin juntes per construir programes interactius.
Algorisme EntradaSortida Definir nom Com Cadena; Escriure "¿Com et dius?"; Llegir nom; Escriure "¡Hola, ", nom, "!";Fin Algorisme10. Eines per treballar amb pseudocodi
PSeInt (acrònim de “PSeudo Intèrpret”) és una aplicació educativa creada amb l’objectiu d’ajudar els estudiants a desenvolupar la lògica algorítmica utilitzant pseudocodi. Es tracta d’un entorn senzill, intuïtiu i en espanyol, cosa que el converteix en una opció valida per a qui comença en aquest camp.
Característiques
- Editor de pseudocodi amb suggeriments i ressaltat de sintaxi.
- Simulador pas a pas, ideal per comprendre el flux d’execució dels algorismes.
- Detecció d’errors comuns i suggeriments per corregir-los.
- Conversió automàtica a altres llenguatges de programació, com Python, Java, JavaScript o C#, per visualitzar com s’implementaria un algorisme en un llenguatge real.
- Suport per a diagrames de flux, que permet representar visualment la lògica abans de codificar-la.
PSeInt permet escriure, simular i validar pseudocodi de forma senzilla, ajudant a entendre la lògica de programació sense preocupar-se per la sintaxi estricta d’un llenguatge específic. A més, inclou altres funcionalitats que permeten transformar pseudocodi en un llenguatge de programació concret.
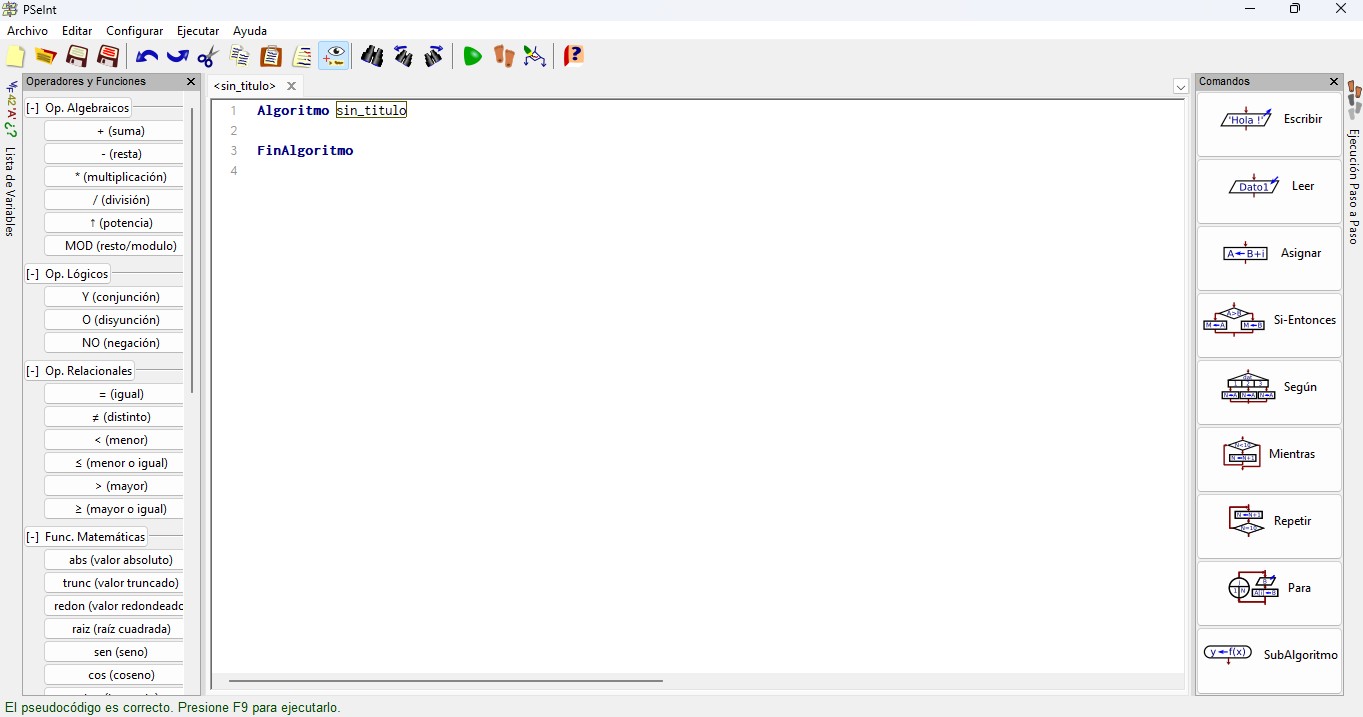
Es pot descarregar des del seu lloc oficial: 👉 https://pseint.sourceforge.net/
11. Exercicis
Exercici 1: Operacions bàsiques
Declara tres variables numèriques: a, b i resultat. Demana a l’usuari que introdueixi els valors de a i b, i després mostra per pantalla la suma, la resta i la multiplicació d’ambdós.
Exercici 2: Operacions per a la figura d’un cercle
Defineix una constant anomenada PI. Demana a l’usuari que introdueixi el radi d’un cercle i calcula la seva àrea utilitzant la fórmula àrea = PI * radi².
Exercici 3: Control de la majoria d’edat
Demana a l’usuari una edat i mostra un missatge que indiqui si és major d’edat o no.
Exercici 4: Login
Demana a l’usuari una contrasenya i verifica si coincideix amb la cadena “1234”. Repeteix la petició fins que encerti.
Exercici 5: Quadrat d’un número
Crea una funció anomenada Quadrat que rebi un número i retorni el seu quadrat. Després, a l’algorisme principal, demana un número a l’usuari, crida la funció i mostra el resultat.
Exercici 6: Saludar Usuari
Defineix un procediment anomenat SaludarUsuari que demani el nom de l’usuari i el saludi. Crida el procediment des de l’algorisme principal.
Exercici 7: Llista de fruites
Crea un vector anomenat fruites amb espai per a 5 elements. Demana a l’usuari que introdueixi els noms de 5 fruites i després mostra la llista completa.
Exercici 8: Taula de multiplicar per 5
Crea una matriu de 10x5 que representi la taula de multiplicar de l’1 al 10. A cada fila s’hi guardarà l’operació a multiplicar, de la següent manera:
| 1 | x | 5 | = | 5 || 2 | x | 5 | = | 10 || 3 | x | 5 | = | 15 |...Mostra la taula completa per pantalla.
🧠 Aquests exercicis són només una petita introducció. Per dominar la lògica de programació, és fonamental seguir practicant de manera constant.
🛠️ Pots trobar més activitats per desenvolupar les teves habilitats al següent enllaç: 👉exercicis👈
